Table of Contents
Lines
by Bitbreaker / Oxyron ^ Arsenic ^ Nuance
Lines can be either calculated using the Bresenham's algorithm, but also by using precalculated slopes. When the lines being used are all short, the number of needed slopes is rather low and memory consumption is less than one might expect. There's also other ways of building lines, like with precalculated tiles or such.
Here's the sourcecode to play around and spoil the experience of doing it all on your own 
Note: To start your compiled line.prg, type SYS 14336 (= $3800). Program doesn't start automatically.

Bresenham
Usually one has to split linedrawing into 4 cases, for that one has to swap coordinates first to achieve that the line end is always lower in y position than the line start. That means we then have lines that will be drawn from bottom to top of the screen. By comparing the dx (x2-x1) and dy (y2-y1) values we can find out if we draw a steep (abs(dx) < dy) or a flat slope (abs(dx) > dy). Thus we end up with those 4 cases:
- flat slope with decrementing y and incrementing on x
- flat slope with decrementing y and decrementing on x
- steep slope with decrementing y and incrementing on x
- steep slope with decrementing y and decrementing on x
The versions for decrementing/incrementing x only differ in the x handling, so after all we have two algorithms that we use, one specialized on steep slopes and one for the flat slopes.
So for steep slopes we always take one y step per pixel, but when our error value overflows we take also a step in x direction. For that we use a mask to cover 8 x steps. So a stepping for e.g. one pixel to the right is just a shift on the mask with lsr mask. The good thing is, when the pixel falls out on the right side, the carry will be set, and thus we know when we bump on the end of our column that we draw in, no matter if we draw on a hires screen or a 16×16 charset grid. In that case we have to do further steps, like adjusting the target where we write the pixels to, as well as resetting the mask to $80 in that case.
Pixel collecting on flat slopes
As for the flat slopes we take a x step for every pixel, but only occasionally do a step in y direction. We could of course add each pixel immedeatedly to the respective memory location, but we could also just remmeber the pixels first and only write them through if we either change column or y-position. Therefore we do the following (x is incrementing in this case):
First, we split up the line into full columns that it covers, the end chunk needs some extra handling. Now we take one column by another to be drawn over. If we start with the leftmost pixel in a column, we start with a mask value of $ff. We keep that mask until we either do a step in y-direction or leave the column. If we leave the column without having had a y-step, we write out $ff and have indeed set 8 pixels with one write. If we have a y change after say 4 pixels, we take the mask, and do a and #$f0 on it and write through 4 pixels. Sounds complex, but as soon as we unroll the code and handle 8 pixels by such an unrolled loop, the initial mask values and values for the and operation are fix.
Means we would have code like this:
ldx #$ff ;start with a full mask
lda err
sbc dy
pixel0
bcc step0 ;underrun @ x & 7 == 0 -> fix y
sbc dy
pixel1
bcc step1 ;underrun @ x & 7 == 1 -> fix y
sbc dy
pixel2
bcc step2 ;underrun @ x & 7 == 2 -> fix y
sbc dy
pixel3
bcc step3 ;underrun @ x & 7 == 3 -> fix y
sbc dy
pixel4
bcc step4 ;underrun @ x & 7 == 4 -> fix y
sbc dy
pixel5
bcc step5 ;underrun @ x & 7 == 5 -> fix y
sbc dy
pixel6
bcc step6 ;underrun @ x & 7 == 6 -> fix y
sbc dy
pixel7
bcc step7 ;underrun @ x & 7 == 7 -> fix y
;no underrun after 8 pixels, write out $ff
lda #$ff
sta (dst),y
...
step0
adc dx ;fix err
sta err
txa ;fetch initial mask
and #$80 ;mask out pixels that need to be written
ora (dst),y
sta (dst),y
lda err ;restore err
dey ;take y step
ldx #$7f
jmp pixel1
step1
adc dx ;fix err
sta err
txa ;fetch initial mask
and #$c0 ;mask out pixels that need to be written
ora (dst),y
sta (dst),y
lda err ;restore err
dey ;take y step
ldx #$3f
jmp pixel2
step2
...
Now when having all unrolled you see that there are several points for optimizations. The case for step0 can be optimized to the following, as in this case always just a single pixel will be set:
adc dx ;fix err
tax
lda #$80 ;mask out pixels that need to be written
ora (dst),y
sta (dst),y
txa ;restore err
dey ;take y step
ldx #$7f
jmp pixel1
Furthermore one can save on the jump and duplicate code:
adc dx ;fix err
tax
lda #$80 ;mask out pixels that need to be written
ora (dst),y
sta (dst),y
txa ;restore err
dey ;take y step
ldx #$7f
sbc dy ;check for underrun
bcs pixel1 ;back to main loop or take another step in y-direction
step1
Third step on optimization is, that one can in that case aggregate the adc dx and sbc dy:
tax
lda #$80 ;mask out pixels that need to be written
ora (dst),y
sta (dst),y
txa ;restore err
dey ;take y step
ldx #$7f
sbc dxdy ;check for underrun. dxdy = dx + 1 - dy (carry is cleared and dy will subtract one too much then again)
bcs pixel1 ;back to main loop or take another step in y-direction
step1
Now seeing that kind of pixel collection one might even go one step further. Actually we can maximum draw 8 pixels until we bump upon a columnchange. That means we can only have 8+7+6+5+4+3+2+1 = 36 different patterns, so why not working out all permutations in code and by that even save on that masking stuff?
f8_new_column_y
ora (dst),y
sta (dst),y
dey
jmp +
;entry point for no y change
f8_new_column
ora (dst),y
sta (dst),y
+
;advance column
tya
eor #$80
tay
bpl +
dec dst+1
+
;... we would also need to check how many full column need to be handled
;... so here'd bea good place to do so
;8 pixels to go
f8_entry
txa
sbc dy
bcc f8_exit_1
sbc dy
bcc f8_exit_2
sbc dy
bcc f8_exit_3
sbc dy
bcc f8_exit_4
sbc dy
bcc f8_exit_5
sbc dy
bcc f8_exit_6
sbc dy
bcc f8_exit_7
sbc dy
bcc f8_exit_8
tax
lda #$ff
jmp f8_new_column+2 ;nothing to ora, as all pixels will be set anyway!
f8_exit_8
adc dx
tax
lda #$ff
jmp f8_new_column_y+2 ;same as above
f8_exit_2
tax
lda #$03
jmp f6_entry_y
f8_exit_3
tax
lda #$07
jmp f5_entry_y
f8_exit_4
tax
lda #$0f
jmp f4_entry_y
f8_exit_5
tax
lda #$1f
jmp f3_entry_y
f8_exit_6
tax
lda #$3f
jmp f2_entry_y
f8_exit_7
tax
lda #$7f
jmp f1_entry_y
f8_exit_1
tax
lda #$01 ;perfect, no jmp needed, just slip through in this case
f7_entry_y
ora (dst),y
sta (dst),y
dey
;7 pixels to go
f7_entry
txa
adc dxdy
bcc f7_exit_1
sbc dy
bcc f7_exit_2
sbc dy
bcc f7_exit_3
sbc dy
bcc f7_exit_4
sbc dy
bcc f7_exit_5
sbc dy
bcc f7_exit_6
sbc dy
bcc f7_exit_7
tax
lda #$fe
jmp f8_new_column
f7_exit_7
adc dx
tax
lda #$fe
jmp f8_new_column_y
f7_exit_2
tax
lda #$06
jmp f5_entry_y
f7_exit_3
tax
lda #$0e
jmp f4_entry_y
f7_exit_4
tax
lda #$1e
jmp f3_entry_y
f7_exit_5
tax
lda #$3e
jmp f2_entry_y
f7_exit_6
tax
lda #$7e
jmp f1_entry_y
f7_exit_1
tax
lda #$02
f6_entry_y
ora (dst),y
sta (dst),y
dey
;6 pixels to go
f6_entry
txa
adc dxdy
bcc f6_exit_1
sbc dy
bcc f6_exit_2
sbc dy
bcc f6_exit_3
sbc dy
bcc f6_exit_4
sbc dy
bcc f6_exit_5
sbc dy
bcc f6_exit_6
tax
lda #$fc
jmp f8_new_column
f6_exit_6
adc dx
tax
lda #$fc
jmp f8_new_column_y
f6_exit_2
tax
lda #$0c
jmp f4_entry_y
f6_exit_3
tax
lda #$1c
jmp f3_entry_y
f6_exit_4
tax
lda #$3c
jmp f2_entry_y
f6_exit_5
tax
lda #$7c
jmp f1_entry_y
f6_exit_1
tax
lda #$04
f5_entry_y
ora (dst),y
sta (dst),y
dey
;5 pixels to go
f5_entry
txa
adc dxdy
bcc f5_exit_1
sbc dy
bcc f5_exit_2
sbc dy
bcc f5_exit_3
sbc dy
bcc f5_exit_4
sbc dy
bcc f5_exit_5
tax
lda #$f8
jmp f8_new_column
f5_exit_5
adc dx
tax
lda #$f8
jmp f8_new_column_y
f5_exit_2
tax
lda #$18
jmp f3_entry_y
f5_exit_3
tax
lda #$38
jmp f2_entry_y
f5_exit_4
tax
lda #$78
jmp f1_entry_y
f5_exit_1
tax
lda #$08
f4_entry_y
ora (dst),y
sta (dst),y
dey
;4 pixels to go
f4_entry
txa
adc dxdy
bcc f4_exit_1
sbc dy
bcc f4_exit_2
sbc dy
bcc f4_exit_3
sbc dy
bcc f4_exit_4
tax
lda #$f0
jmp f8_new_column
f4_exit_4
adc dx
tax
lda #$f0
jmp f8_new_column_y
f4_exit_2
tax
lda #$30
jmp f2_entry_y
f4_exit_3
tax
lda #$70
jmp f1_entry_y
f4_exit_1
tax
lda #$10
f3_entry_y
ora (dst),y
sta (dst),y
dey
;3 pixels to go
f3_entry
txa
adc dxdy
bcc f3_exit_1
sbc dy
bcc f3_exit_2
sbc dy
bcc f3_exit_3
tax
lda #$e0
jmp f8_new_column
f3_exit_3
adc dx
tax
lda #$e0
jmp f8_new_column_y
f3_exit_2
tax
lda #$60
jmp f1_entry_y
f3_exit_1
tax
lda #$20
f2_entry_y
ora (dst),y
sta (dst),y
dey
;2 pixels to go
f2_entry
txa
adc dxdy
bcc f2_exit_1
sbc dy
bcc f2_exit_2
tax
lda #$c0
jmp f8_new_column
f2_exit_2
adc dx
tax
lda #$c0
jmp f8_new_column_y
f2_exit_1
tax
lda #$40
f1_entry_y
ora (dst),y
sta (dst),y
dey
;1 pixel to go
f1_entry
txa
adc dxdy
bcc f1_exit_1
tax
lda #$80
jmp f8_new_column
f1_exit_1
adc dx
tax
lda #$80
jmp f8_new_column_y
If we precalculate the linecoordinates beforehand, we can now even give each line a flag if it collides with any other line, else we can even forgo on the ora (dst),y component! depending on the first pixel x-position we just enter that code depending on x & 7 on either f8_entry, f7_entry, f6_entry, …
Steep slopes
Examples for the steep slopes can be found here. Also one can unroll things in the same manner as for the flat slopes regarding permutations, just that we aim for different run lengths and not for patterns.
With a loop
One can use the advantage of some illegal opcodes to make a looped version nearly as fast as an unrolled variant. In fact the inner loop here is one cycle faster then the method being used in The Masque. However the overhead that arises from shifting the pixelmask and advancing the pointers dst1 + dst2 is wasting more cycles then with an unrolled line drawing routine. So if you want it fast but also need to save memory, this is what you want:
back_
rol mask
back
pix lda #$00
dst1 ora $2000,y
dst2 sta $2000,y
dey
bpl out ;anoying, but needed in a loop variant
txa
dx sbx #$00
bcs back
move_x
txa
dy sbx #$00 ;add dy (by subtracting -dy)
lda (dst1),y
slo pix ;shift mask and ora mask with value @ dst1
bcc dst2 ;column change? no -> do it the short way
lda #$80
eor dst1+1
sta dst1+1
sta dst2+1
bmi back_
inc dst1+2
inc dst2+2
lda #$01
sta mask
bne back+2
Needless to say that this code is best placed into zeropage for maximum performance. The addition of dy and the next upcoming subtract can again be aggregated and additional cycles can be saved that way.
Unrolled
Unrolling the above code brings two advantages: One does not have to check for the underrun of Y, and one can use absolute adressing. The tradeoff: sbx can't be used anymore and one needs to use sbc dx/adc dy to calculate the slope, what wastes more cycles. Also one needs to find the sweet spot between saved cycles and memory consumption.
-
tax
lda #$01
ora $2780,y
sta $2780,y
dey
txa
sbc dx
bcs - ;2+2+4+5+2+2+3+3 = 23 cycles per pixel
adc dy ;but overhead is at a minimum
-
tax
lda #$02
ora $2780,y
sta $2780,y
dey
txa
sbc dx
bcs -
adc dy
...
Memory consumption is 2176 bytes (17 bytes * 8 pixels * 16 columns). However this method forces us to do an extra handling for the last x-position on each line, to land on the right Y value.
If you can afford a lot of memory you might think of a fully unrolled variant that unrolles each possible column:
tay
lda $277f
sax $277f
tya
sbc dx
bcs ++ ;ossom 18 cycles per pixel!
adc dy
tay
txa
rol
bcs +
rol
jmp column15_y7e ;change column, jump into unrolled loop of adjacent column
+
tax
++
tay
lda $277e
sax $277e
tya
sbc dx
bcs ++
adc dy
tay
txa
rol
bcs +
rol
jmp column15_y7d
+
tax
++
...
This method would work on inverted graphics, means it does not plot but delete pixels, thus we can make use of the SAX command, but for that have to get rid of the y-index. However memory consumption is tremendous now: 24 * 16 * 128 = $c000 bytes. However there's a lot of dead code there. Especially at the outer columns there's no need to unroll all 128 lines, as you object will rotate and draw within a circle, it is enough to only support those bytes that are within that circle, no lines will be drawn outside of it. So it would be around 4 / PI * $c000 bytes.
If you dare to flip x and y axis on the 16×16 grid, also the following would be possible:
loop_14_bit1_y7
tax
lda #$01
ora $2707,y
sta $2707,y
txa
sbc dy
bcc +
loop_14_bit1_y6
tax
lda #$01
ora $2706,y
sta $2706,y
txa
sbc dy
bcc ++
loop_14_bit1_y5
tax
lda #$01
ora $2705,y
sta $2705,y
txa
sbc dy
bcc +++
loop_14_bit1_y4
tax
lda #$01
ora $2704,y
sta $2704,y
txa
sbc dy
bcc ++++
loop_14_bit1_y3
tax
lda #$01
ora $2703,y
sta $2703,y
txa
sbc dy
bcc +++++
loop_14_bit1_y2
tax
lda #$01
ora $2702,y
sta $2702,y
txa
sbc dy
bcc ++++++
loop_14_bit1_y1
tax
lda #$01
ora $2701,y
sta $2701,y
txa
sbc dy
bcc +++++++
loop_14_bit1_y0
tax
lda #$01
ora $2700,y
sta $2700,y
txa
sbc dy
bcc ++++++++
tax
tya
eor #$80
tay
bpl loop_14_bit1_y7+1
jmp loop_12_bit1_y7+1
+
adc dx
jmp loop_14_bit2_y6
++
adc dx
jmp loop_14_bit2_y5
+++
adc dx
jmp loop_14_bit2_y4
++++
adc dx
jmp loop_14_bit2_y3
+++++
adc dx
jmp loop_14_bit2_y2
++++++
adc dx
jmp loop_14_bit2_y1
+++++++
adc dx
jmp loop_14_bit2_y0
++++++++
adc dx
tax
tya
eor #$80
tay
bpl loop_14_bit2_y7+1
jmp loop_12_bit2_y7+1
loop_14_bit2_y7
tax
lda #$02
ora $2707,y
sta $2707,y
txa
sbc dy
bcc +
;...
loop_12_bit1_y7
tax
lda #$01
ora $2607,y
sta $2607,y
txa
sbc dy
bcc +
;...
Now you can unroll the loop for 16 (or better 8, if you choose to cover 2 rows by using Y & $7f or Y | $80) rows of chars and handle 8 lines per charline continously. Also the code needs to be unrolled per X shift. Whenever the pixelmask wraps around, one needs to subtract another 8 from Y, not too much of a compelx handling, but therefore with somewhat 20 cycles for setting a pixel. The flat version will therefore need some etxtra handling on changing a charrow, but as that is happening rather seldom it should not matter much.
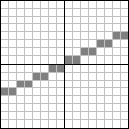
Run length slice
 Seeing the depicted line, one can notice that there's either 2 or 3 pixels set. So when doing an abs(dy/dx) we get the minimum number of pixels being set. So if we have a steep line with dx = 19 and dy = 80 we would always draw either 4 or 5 consecutive pixels before a x-step would occur.
However dividing is expensive, but one could stick to divide into cases that fit within a power of 2. The decision would work like this:
Seeing the depicted line, one can notice that there's either 2 or 3 pixels set. So when doing an abs(dy/dx) we get the minimum number of pixels being set. So if we have a steep line with dx = 19 and dy = 80 we would always draw either 4 or 5 consecutive pixels before a x-step would occur.
However dividing is expensive, but one could stick to divide into cases that fit within a power of 2. The decision would work like this:
lda dx
asl
cmp dy
bcs do_1_or2
asl
cmp dy
bcs do_2_or3
asl
cmp dy
bcs do_4_or5
asl
cmp dy
bcs do_8_or9
...
As for the unrolled loop you could do something like:
!align 255,0
entry_9
lda d_pixm
ora (d_dst1),y
sta (d_dst1),y
dey
bmi dout
entry_8
lda d_pixm
ora (d_dst1),y
sta (d_dst1),y
dey
bmi dout
entry_7
lda d_pixm
ora (d_dst1),y
sta (d_dst1),y
dey
bmi dout
entry_6
lda d_pixm
ora (d_dst1),y
sta (d_dst1),y
dey
bmi dout
entry_5
lda d_pixm
ora (d_dst1),y
sta (d_dst1),y
dey
bmi dout
entry_4
lda d_pixm
ora (d_dst1),y
sta (d_dst1),y
dey
bmi dout
entry_3
lda d_pixm
ora (d_dst1),y
sta (d_dst1),y
dey
bmi dout
entry_2
lda d_pixm
ora (d_dst1),y
sta (d_dst1),y
dey
bmi dout
txa
dx_mul sbx #$00
bcc + ;all done, or is another single one needed?
entry_1
lda d_pixm
ora (d_dst1),y
sta (d_dst1),y
dey
bmi dout
txa
dx_sin sbx #$00
bcs entry_1
+
asl d_pixm ;advance pixel
bcc +
;change column
rol d_pixm
lda #$80
eor d_dst1
sta d_dst1
bpl +
dec d_dst1+1
+
txa
adc dy
tax
jmp_e jmp dstart ;will be modified to point to entry_* depending on how many pixel in a row need to be set
dout
rts
Now with the dependencies of the run length slice method in mind, one can also improve the flat line algorithm mentioned before again. Taking f8_exit_4 as an example, we can assume that we successfully drew 4 pixels. That means that 4 pixels is the minium or maximum pixels to draw. Thus we are safe to aggregate the sbc for the next upcoming three pixels by doing:
f8_exit_4
adc dxdy
sbc dy ;still no underrun will occur
tax
lda #$0f
ora (dst),y
sta (dst),y
dey
txa
jmp f4_entry+9 ;3rd sbc there + branch
The case f8_exit_5 makes it even easier for us, as we can finish the column at the same time:
f8_exit_5
adc dxdy
sbc dy
sbc dy
tax
lda #$1f
ora (dst),y
sta (dst),y
dey
lda #$e0
jmp f8_new_column
As you can see, we can aggregate the subtractions already beforehand and plot the next and last chunk within this column.
To some amount the runlength slice paradigm could also be applied to certain parts of the steep slopes. Imagine you calculate the lines within blocks of 8×8 pixels. On steep slopes thus, maximum 8 x steps can occur during 8 y steps. Thus, when our slope once leaves the current column to the left or right, on the next column one can forgo on the column checks, as the column will not be changed once more until the upper or lower border of the block is reached.
Overhead
Splitting things up into a big bunch of algorithms sometimes look like a good idea as each algorithm can then be maxed out. But on the other hand all the decisions have to be done for each single line, and easily consume the few saved cycles of a special case that only happens each now and then. It is wise to keep track of the optimization one does by benchmarking each new try. Thus it is easy to decide if a change is wort the few cycles for lots of additional code, or if the changes even slow things down.
Going fullscreen
Having lines in a 16×16 square is nice, but how's about going fullscreen finally? One might think that this means a lot of pain, for a bunch of good reasons:
- x-coordinates can have a delta bigger than 255, no one loves 16 bit calculations on a 8 bit machine
- addressing of blocks in a bitmap is more complex than within a 16×16 grid, where each column can be addressed linear
- clearing the whole bitmap is no option, there needs to be a better concept
Luckily, there's also a bunch of good solutions to all those bothers!
As for x-coordinates, lines usually do not get that big lengths if you keep your model fairly complex, if it would really happen, just cut the line into two halves and draw 2 shorter lines. This however only applies to dx/dy, x-coordinates still need to be handled with 9 bits on a 320×200 screen. But the hassle with those is less than expected, you'll see!
As for the other two problems we can take advantage of the fact, that we use a screen together with a bitmap. When ink and paper on screen are set with the background color, the corresponding block of the bitmap is made “invisible”, as both background and drawn content are displayed in the same color. So clearing can be done by just writing for e.g. $00 to the whole screen to camouflage the bitmap content. When drawing lines we would however need to also set the screen to make our blocks appear again. Cumbersome on the one hand, but also a cool thing, as we have by that a map of dirty blocks, on which we can do further optimizations. So what we do is walking relatively on a screen and bitmap, for that we use 2 pointers. One for the screen and one for the bitmap. For each direction the pointers are manipulated respectively. Also we would now be able to give each line a different colour (but of course would need to avoid clashes).
Thus, when we leave a block and enter a new block, we can now make decisions while consulting our map. If we enter a used block, we will need to merge in our new content the classic way (by using ora), but if we are on a pristine block, we can simply write through our new pixels without the need of ora. However we need to wipe out the lines of the block that we don't use, as they might contain garbage from older renderings, that would become visible on “turning on” that char in the map.
Charmode
Now we could even go a step further and move that concept of a map over to charmode (see image with visualized screen that represents the final image). Here we have an easier handling as on every new block that we start just need to advance the charset pointer by 8. Also we would just need a forth of the space a regular bitmap would consume. However we are limited to 256 chars only, but to reach that margin you need very huge and complex objects. The objects in Comaland use a maximum of 192 chars, so that there are another 63 chars left for the logo and a clear char can be reserved. Of course you are also free to work with several charsets and split the screen vertically. But then even more complexity applies. Better start with a single charset first.
So how would all this work? First, we take an empty charset and define char $00 as an empty char, we fill the screen with $00 and wipe out the first 8 bytes of our charset. Thus we start with an empty srceen.
Now we draw the first line, render it block by block (dx / 8 and dy / 8). Due to that, a lot of optimizations like run length encoding can be applied, in x- and now even in y-direction! (more on that later) Whenever we leave a block, we decide on how to render the next block and what area we need to clear. If we move from a pristine block to another pristine block, we can best case clear 8 lines in a row (in 50% of the cases this can be optimized to 8 bytes being cleared linearly!). On leaving a pristine block, we also place the current char number on the screen, then we advance the char pointer and the char number to be used. The screen pointer will be bumped in any case to be able to access teh next block info, as the screen also acts as map for used blocks. Sounds complex but actually the following code snippets look rather simple, right?
;check current block type
lda (screen,x) ;assume x = 0
beq no_ora_needed
ora_needed
inc_screen_pointer
inc scr
bne *+4
inc scr+1
dec_screen_pointer
lda #$ff
dcp scr ;compare + force carry always set
bne *+4
dec scr+1
So when we observe this pic, the workflow would be like the following:
Draw 2 pixels in one go until we leave the block either at the top or right side. Upon leaving we recognize due to the position in our unrolled code that we rendered until y = 3, so there's 3 lines below to clear, upon entering the next block we recognize by the position in our unrolled code that we start with y = 3, means we have to clear the 5 lines to the bottom of the block. As it is a pristine block, we can continue with write through mode and forgo on using ora.
Upon entering a dirty block that is already in use, we switch to ora mode. For that we pick the screen code and multiply it by 8 (+offset) to have the resulting pointer into the charset, a lookup table makes things easier and faster.
More examples (green ares need to be cleared):
Same but for a flat slope with decrementing y
Flat sloop with incrementing y
A special case were nothing needs to be cleared
Lines to be cleared when entering an already used block (ora is used from there on)
Optimizations in y-direction.
The steep lines can be unrolled with ease, as we would maximum handle 8 lines in the unrolled code, as then a new block starts, the code would however also work in linear columns as being used with a 16×16 grid, but possibly checks on y need to be applied or things need to be draw blockwise as well. By unrolling the subtraction of dx can be handled before drawing pixels, then upon underflow n rows will be filled with the same value in one go. Thus the error does not need to be saved and restored per step, but per x step, and the bitmask also just needs to be loaded once per x step, while it can be shifted in an easier fashion too. Also, if a pixel was drawn for e.g. 4 times before, the next step can be simplified and 3 times dx already be subtracted without any check, in certain cases even all left pixels can be drawn without any further checks, as the next line segment must be either 3, 4 or 5 pixel long, depending if we just drew the minimum or maximum of pixels per chunk. This is, due to the fact, that we draw a fixed amount of pixels per step + 1 additional pixel from time to time to cope with the error, so a line would typically be drawn like:
X
X
X
X
X
X
X
X
X
X
X
X
X
or
X
X
X
X
X
X
X
X
X
X
So we can in the next step at least expect 3 pixels in a row, no matter if we follow the upper example where 4 pixels would be our minimum or the lower example where 4 pixels would be our maximum.
The said optimizations are only available in the write through mode and not if the new content needs to be ora'd in.
Upcoming a code snippet that expresses the said:
dec8_no_ora_entry
txa ;fetch error
;8 lines to check
sbc dx
bcc dec8_exit_1 ;overflow on 1st line, 7 lines to go
sbc dx
bcc dec8_exit_2 ;overflow on 2nd line, 6 lines to go
sbc dx
bcc dec8_exit_3 ;overflow on 3rd line, 5 lines to go
sbc dx
bcc dec8_exit_4 ;...
sbc dx
bcc dec8_exit_5
sbc dx
bcc dec8_exit_6
sbc dx
bcc dec8_exit_7
sbc dx
tax
lda mask ;perfect match, write mask 8 times in one run
sta (cset),y
dey
sta (cset),y
dey
sta (cset),y
dey
sta (cset),y
dey
sta (cset),y
dey
sta (cset),y
dey
sta (cset),y
dey
jmp dupdate_y_s_ ;advance to next block
And one exit point as example:
dec8_exit_5
tax ;save error
lda mask ;write 5 pixels in a row
sta (cset),y
dey
sta (cset),y
dey
sta (cset),y
dey
sta (cset),y
dey
sta (cset),y
dey
asl ;shift mask
bcs + ;column change?
;3 sbcs won't underrun for sure, so we can draw the upcoming three dots without any further checks \o/
sta (cset),y
dey
sta (cset),y
dey
sta (cset),y
sta mask ;remember mask
txa
adc+1 dydx ;add dy and do three sbc dx without harm (you remember, we can't underrun so far)
sbc+1 dx
sbc+1 dx
tax
jmp dupdate_y_s ;block change, all done
+
jmp dec_clear_3 ;preliminary column change, need to wipe 3 lines
Clearing
As described, clearing can be done by simply wiping out the used screen. There's also the option to wipe out the charset until the last used char on each frame and forgo on the clearing per block. In practice it showed that the clearing on a block basis however performs already pretty fast. In case one would need unrolled code that is entered at the right offset, what will be quite costly with double buffering. For a faster clearing of the srceen one can log the screen per frame and thus build up a map of overall used blocks during the whole effect. Unused blocks do not need to be cleared over all. This makes the resulting speedcode faster and smaller and allows for clipped overlayed objects like the logo.