base:approximation_to_distance
Classic distance formula is d= SQR( (x2-x1)^2 + (y2-y1)^2)) and it is well known that if you are comparing the magnitude of two distances you can avoid doing the square root operation as the square of the distances sort in the same order. However, to avoid the square root and the multiplication is the intent of this approximation.
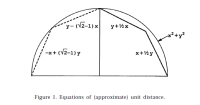
The following approximation is based on a combination of linear components of the min and max functions.
The formula is d = max(|xd|, |yd|) + 1/2 × min(|xd|, |yd|) where xd = (x1-x2) and yd = (y1-y2)
Note that for 6502 we will use a shift right to calculate the multiply by 1/2.
; gives approximate distance from (x1,y1) to (x2,y2) ; with only overestimations, and then never by more ; than (9/8) + one bit uncertainty. ; input: x1,y1 x2,y2 ; uses: A xd,yd ; output: approximate distance between x1,y1 and x2,y2 in A + ninth bit in C ; If the actual distance is 228 or less the result estimate will fit in 8 bits Dist: lda x1 sec sbc x2 sta xd bcs posxdiff eor #$FF adc #1 posxdiff: sta xd lda y1 sec sbc y2 bcs posydiff eor #$FF adc #1 posydiff: cmp xd bcs ygreater lsr clc adc xd rts ygreater: lsr xd clc adc xd rts
derivation: A FAST APPROXIMATION TO THE HYPOTENUSE page 427 of Graphics Gems 1
base/approximation_to_distance.txt · Last modified: 2020-02-11 01:45 by djmips